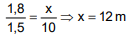Moda para datos agrupados

¿Qué es Moda para datos agrupados?

Es el valor que representa la mayor frecuencia absoluta. En tablas de frecuencias con datos agrupados, hablaremos de intervalo modal.

Fórmula para calcular la moda para datos agrupados:

Todos los intervalos tienen la misma amplitud.

Li Extremo inferior del intervalo modal (intervalo que tiene mayor frecuencia absoluta).

fi Frecuencia absoluta del intervalo modal.

fi-1 Frecuencia absoluta del intervalo anterior al modal.

fi+1 Frecuencia absoluta del intervalo posterior al modal.

ti Amplitud de los intervalos.

Ejercicio: Calculemos la moda Mo :

Leer más

MEDIDAS DE TENDENCIA CENTRAL PARA DATOS AGRUPADOS

Medidas de tendencia central para datos agrupados "MEDIA ARITMÉTICA"

¿Cuándo utilizar las medidas de tendencia central para datos agrpados?

Cuando se trabaja con datos que han sido agrupados en una distribución de frecuencias, no se sabe con certeza los valores individuales de cada dato. Por lo que se utilizan métodos alternos para aproximar los valores de las medidas descriptivas.

Fórmula para calcular la media aritmética para datos agrupados:

Ejemplo: media aritmética para datos agrupados en tablas:

En un test realizado a un grupo de 42 personas se han obtenido las puntuaciones que muestra la tabla. Calcula la puntuación media

Vídeo de como calcular la Media Aritmética para datos agrupados:

Leer más

MODA ESTADÍSTICA

Moda

¿Qué es la Moda en Estaística?

La moda es una medida de tendencia central que indica el valor que más se repite en un grupo de números. En un mismo estudio puede haber más de una moda, esto ocurre cuando dos (bimodal) o más números (multimodal) se repiten la misma cantidad de veces siendo este es el máximo número de veces del conjunto.

¿Cómo calcular la moda en estadística?

*Ordena los números según su tamaño.

*Determina la cantidad de veces de cada valor numérico.

*El valor numérico que más se repite es la moda.

*Puede haber más de una moda cuando dos o más números se repiten la misma cantidad de veces y además este es el máximo número de veces del conjunto.

*No hay moda si ningún número se repite más de una vez.

Símbolo de la moda

La moda es una medida que se relaciona con la frecuencia en la que aparece un dato en un supuesto. La moda puede aparecer tanto en datos cualitativos como cuantitativos. La moda Estadística se representa de forma: Mo

Ejemplo de la moda estadística:

Calcular la moda de la siguiente serie de números: 5, 3, 6, 5, 4, 5, 2, 8, 6, 5, 4, 8, 3, 4, 5, 4, 8, 2, 5, 4.

Mo = 5

Ilustración con ejercicio de la Moda Estadística:

Leer más

MEDIANA

Mediana

La mediana es el valor de la variable que ocupa la posición central, cuando los datos se disponen en orden de magnitud. Es decir, el 50% de las observaciones tiene valores iguales o inferiores a la mediana y el otro 50% tiene valores iguales o superiores a la mediana.

¿Cuándo se utiliza la Mediana?

La mediana se utiliza generalmente para devolver la tendencia central en el caso de distribuciones numéricas sesgadas.

¿Cómo se calcula la Mediana?

La mediana se puede calcular poniendo los números en orden ascendente y luego localizando el número del centro de esa distribución.

Ejemplos en donde se calcula la Mediana:

1. Encuentre la mediana del conjunto {2, 5, 8, 11, 16, 21, 30}

Hay 7 números en el conjunto, y estos están acomodados en orden ascendente. El número medio (el cuarto en la lista) es 11. Así, la mediana es 11.

2. Las edades de un grupo de esudiantes son: {13, 15, 18, 19, 21, 26, 28, 33, 35}

Hay 9 números en el conjunto, y estos están acomodados en orden ascendente. El número medio (el quinto en la lista) es 21. Así, la mediana es 21.

Leer más

Media Aritmética

¿Qué es Media Aritmética?

En matemáticas y estadística una media o promedio es una medida de tendencia central. Resulta al efectuar una serie determinada de operaciones con un conjunto de números y que, en determinadas condiciones, puede representar por sí solo a todo el conjunto».

Leer más

MEDIDAS DE TENDENCIA CENTRAL

Medidas de tendencia central y dispersión

Las medidas de tendencia central son medidas estadísticas que pretenden resumir en un solo valor a un conjunto de valores. Representan un centro en torno al cual se encuentra ubicado el conjunto de los datos.

Las medidas de tendencia central más utilizadas son

*Media

*Mediana

*Moda

Las medidas de dispersión en cambio miden el grado de dispersión de los valores de la variable. Dicho en otros términos las medidas de dispersión pretenden evaluar en qué medida los datos difieren entre sí. De esta forma, ambos tipos de medidas usadas en conjunto permiten describir un conjunto de datos entregando información acerca de su posición y su dispersión.

¿Para que sirven las medidas de tendencia central?

Son empleadas para resumir a los conjuntos de datos que serán sometidos a un estudio estadístico, se les llama medidas de tendencia central porque general mente la acumulación más alta de datos se encuentra en los valores intermedios.

Leer más

Desviación Típica

¿Qué es Desviación Típica?

La desviación típica o desviación estándar (denotada con el símbolo σ o s, dependiendo de la procedencia del conjunto de datos) es una medida de dispersión para variables de razón (variables cuantitativas o cantidades racionales) y de intervalo.

Características de la Desviación Típica

*El monto diferido entre los datos y el promedio, se mide como un resultado positivo o igual a cero (siendo igual a cero cuando no hay variación entre los datos obtenidos).
*Es igual de aplicable si los datos son mayores o menores que el promedio.
*No es el promedio de las diferencias.

¿Cómo calcular la Desviación Típica?

Leer más

Rango

¿Qué es Rango?

El Rango es el intervalo entre el valor máximo y el valor mínimo; por ello, comparte unidades con los datos. Permite obtener una idea de la dispersión de los datos, cuanto mayor es el rango, más dispersos están los datos (sin considerar la afectación de los valores extremos).

Pasos para encontrar el rango

*Ordena los números según su tamaño.
*Resta el valor mínimo del valor máximo.

Ejercicios de aplicación Encontrando el Rango

1.Determine el rango, de los siguientes conjuntos de números: 232, 212, 151, 325, 142, 132, 142, 236, 145

Solución:

Se Ordenan: 132, 142, 142, 145, 151, 212, 232, 236, 325

El mínimo es 132 y el máximo es 325

Rango = [132, 325]

2.Determine el rango, de las edades que tienen los estudiantes de Estadística: 22, 21, 17, 32, 19, 18, 25, 26, 24

Solución:

Se Ordenan: 17, 18, 19, 21, 22, 24, 225, 25, 32

El mínimo es 17 y el máximo es 32

Rango = [17, 32]

Leer más

MEDIDAS DE DISPERSIÓN

Medidas de dispersión

Las medidas de dispersión muestran la variabilidad de una distribución, indicándolo por medio de un número, si las diferentes puntuaciones de una variable están muy alejadas de la media.

Carateristicas de las médidas de dispersión

• Las medidas de dispersión nos sirven para cuantificar la separación de los valores de una distribución.

• Al calcular una medida de centralización como es la media aritmética, resulta necesario acompañarla de otra medida que indique el grado de dispersión, del resto de valores de la distribución, respecto de esta media.

• Llamaremos DISPERSIÓN O VARIABILIDAD, a la mayor o menor separación de los valores de la muestra, respecto de las medidas de centralización que hayamos calculado.

Ejemplos de las médidas de dispersión

•Rango

•Desviación Media

•Varianza

•Desviacion Típica

Leer más

APLICACIÓN AL ENTORNO DE LOS TRIÁNGULOS SEMEJANTES

APLICACIÓN AL ENTORNO DE LOS TRIÁNGULOS SEMEJANTES

Cuando usar el término semejanza en la vida cotidiana

*Un objeto que se parece a otro.

*Objetos de igual tamaño.

*Objetos de igual forma.

*Objetos exactamente iguales.

Ejemplos de semejanza de triángulos en la vida cotidiana

1. A cierta hora del día, Mario y Jennifer se colocan de pie en el patio de su escuela. Mario proyecta una sombra de 90 cm de longitud, mientras que la sombra de Jennifer mide 75 cm de longitud. Si la estatura de Mario es 1.80 m, ¿cuál es la estatura de Jennifer?

2. La sombra de una torre eléctrica mide 10 m y en el mismo instante, la sombra de un joven mide 1,5 m. Si el joven tiene una altura de 1,8 m, ¿cuál es la altura de la torre?

Solución: Los triángulos formados por la torre y su sombra y por el joven y su sombra son semejantes, pues los rayos de sol son paralelos.

Por lo tanto, X representa la altura de la Torre y es de 12 m.

Leer más

TRIÁNGULOS SEMEJANTES

TRIÁNGULOS SEMEJANTES

¿Qué es semejanza de trángulos?

La semejanza de triángulos es una característica que hace que dos o más triángulos sean semejantes. Dos triángulos son semejantes cuando tienen sus ángulos iguales (o congruentes) y sus lados correspondientes (u homólogos) son proporcionales.

Criterios de semejanza de dos triángulos

*Que tengan dos ángulos iguales.

*Que tengan dos lados proporcionales y el ángulo comprendido entre ellos sea igual.

*Que tengan sus tres lados correspondientes proporcionales.

Imágenes del entorno donde se observa Semejanza de Triangulos

A continuación, te reto a armar este rompecabeza ¿Quiéres intentarlo? Click aquí

#Rompecabezasdetriángulossemejantes

¡Buena suerte!

Leer más

ECUACIONES DE SEGUNDO GRADO

Ecuaciones de segundo grado

¿Qué es ecuación de segundo grado?

Son ecuaciones de segundo grado aquellas en las que la incógnita aparece al menos una vez elevada al cuadrado (x^2 ).

La ecuación de segundo grado se puede expresar de la forma:

Donde a, b y c serán números enteros (positivos o negativos). Para ello bastará obtener el denominador común (si hay denominadores), para eliminarlo y pasar todos los términos al primer miembro.

Sabemos que una vez conseguida dicha forma, las dos "posibles" soluciones de la ecuación son:

Ejercicios de aplicación usando Ecuaciones de Segundo Grado

Dentro de 11 años la edad de Pedro será la mitad del cuadrado de la edad que tenía hace 13 años. Calcula la edad de Pedro.

Para vallar una finca rectangular de 750 m² se han utilizado 110 m de cerca. Calcula las dimensiones de la finca

Vídeo de Ecuaciones de Segundo Grado:

Leer más

ECUACIONES DE PRIMER GRADO

Ecuaciones de primer grado

¿Qué es ecuación de primer grado?

Se dice que son de primer grado cuando dicha letra no está elevada a ninguna potencia (por tanto, a 1).

Pasos para resolver ecuaciones de primer grado:

1.Agrupa los números a un lado del símbolo = todos los términos que tengan la incógnita (x) y junta en el otro todos los términos que no tienen (x).

2.Resuelve de forma separada las operaciones de cada lado del igual. Es decir, para resolver la ecuación de primer grado deber formular las operaciones hasta dejar un número a cada lado del igual.

3.Finalmente, para resolver la ecuación de primer grado el número que está multiplicando a la x pasa a dividir el valor del otro lado del igual.

Ejemplos de la vida cotidiana con Ecuaciones de Primer grado:

Se desean repartir 290 naranjas entre Juan y Pedro de forma que Pedro reciba 40 más que Juan. ¿Cuántas naranjas le corresponden a cada uno?

Una laguna tiene 1200 m de perímetro, Ana corre a una velocidad de 140 m/min en dirección horaria, mientras que José corre a una velocidad de 160 m/min en sentido antihorario. Si ambos salen del mismo punto al mismo tiempo, ¿en cuántos minutos se vuelven a encontrar?

Vídeo de Ecuaciones de Primer Grado:

Leer más

SISTEMA DE ECUACIONES

SISTEMA DE ECUACIONES

¿QUÉ ES UN SISTEMA DE ECUACIONES LINEALES?

Un sistema de ecuaciones lineales es un conjunto de ecuaciones (lineales) que tienen más de una incógnita. Las incógnitas aparecen en varias de las ecuaciones, pero no necesariamente en todas. Lo que hacen estas ecuaciones es relacionar las  incógnitas entre sí.

TIPOS DE SISTEMAS DE ECUACIONES LINEALES

Los sistemas de ecuaciones se pueden clasificar según el número de soluciones que pueden presentar. De acuerdo con ese caso se pueden presentar los siguientes casos:

·         Sistema compatible si tiene solución, en este caso además puede distinguirse entre:

·         Sistema compatible determinado cuando tiene una única solución.

·         Sistema compatible indeterminado cuando admite un conjunto infinito de soluciones.

·         Sistema incompatible si no tiene solución.

MÉTODOS QUE SE PUEDEN PARA LA RESOLUCIÓN DE LOS SISTEMAS DE ECUACIONES

Sustitución

El método de sustitución consiste en despejar en una de las ecuaciones con cualquier incógnita, preferiblemente la que tenga menor coeficiente y a continuación sustituirla en otra ecuación por su valor.

Igualación

El método de igualación se puede entender como un caso particular del método de sustitución en el que se despeja la misma incógnita en dos ecuaciones y a continuación se igualan entre sí la parte derecha de ambas ecuaciones.

Reducción

Este método posee un procedimiento, diseñado para sistemas con dos ecuaciones e incógnitas, consiste en transformar una de las ecuaciones (generalmente, mediante productos), de manera que obtengamos dos ecuaciones en la que una misma incógnita aparezca con el mismo coeficiente y distinto signo.

Método gráfico

Consiste en construir la gráfica de cada una de las ecuaciones del sistema. El método (manualmente aplicado) solo resulta eficiente en el plano cartesiano, es decir para un espacio de dimensión.

Método de Gauss 

El método de eliminación de Gauss o simplemente método de Gauss consiste en convertir un sistema lineal de n ecuaciones con n incógnitas, en uno escalonado, en el que la primera ecuación tiene n incógnitas, la segunda ecuación tiene n - 1 incógnitas, ..., hasta la última ecuación, que tiene 1 incógnita.

Leer más

PROPORCIONALIDAD INVERSA.

PROPORCIONALIDAD INVERSA.

Dos magnitudes son inversamente proporcionales cuando:

✔ Al aumentar un valor, el otro disminuye en la misma proporción.
✔ Al disminuir un valor, el otro aumenta en la misma proporción.

Cómo efectuar una proporcionalidad inversa paso a paso:

Si para un valor A de una magnitud, tenemos un valor B de la otra magnitud, para un valor de C de la primera magnitud, a la segunda magnitud le corresponderá un valor de X:

¿Cuánto vale esa X?

En una proporcionalidad inversa, la X se calcula multiplicando los dos valores que están en la línea donde no está la X, divididos entre el valor que se encuentre en la misma línea que la X. Para acordarnos, se dice que la X se resuelve en línea (a diferencia de la proporcionalidad directa que es en cruz):

La fórmula sería:

Ejemplos de proporcionalidad inversa, aplicados a el entorno.

1. Si 2 agricultores tardan 10 días en arar un campo, ¿cuánto tardarán agricultores en realizar el mismo trabajo?

Es decir, mientras que dos agricultores tardan 10 días, con la ayuda de otros compañeros consiguen hacer el mismo trabajo en tan solo 4 días.

2. Un grifo con un determinado caudal tarda 30 minutos en llenar un depósito. ¿Cuántos minutos tardaría en llenarse el depósito con 3 grifos con el mismo caudal?

Esto quiere decir que a mayor cantidad de grifos, menos tiempo se tardara en llenar los depósitos.

A continuación se presenta un vídeo ilustrativo, el cual enseña de la proporcionalidad:

Leer más